I present a few systematic strategies for investing into volatility risk-premia and illustrate their back-tested performance. I apply the four factor Fama-French-Carhart model to attribute monthly returns on volatility strategies to returns on the style factors. I show that all strategies have insignificant exposure to the style factors, while the exposure to the market factor becomes insignificant when strategies are equipped with statistical filtering and delta-hedging. I show that, by allocating 10% of portfolio funds to these strategies within equity and fixed-income benchmarked portfolios, investors can boost the alpha by 1% and increase the Sharpe ratio by 10%-20%.
It is becoming acknowledged that volatility strategies should constitute an integral part of allocation to alternatives in portfolios of institutional and HNW investors. Indeed, both the academic and the practical experience indicate that volatility strategies produce robust risk-adjusted long-term performance, when properly designed and executed.
The growing investors’ demand for transparent solutions has been recently met by algorithmic strategies and exchange-traded funds offered by major institutions. These algorithmic strategies provide multiple solutions to invest and allocate to volatility strategies in a direct and transparent way. Yet, investors and allocators must make the ultimate decision about selecting and allocating to appropriate investment solutions.
Importantly, investors need to carefully consider the following aspects by allocating to volatility strategies:
- The design of a systematic strategy, which most importantly includes what instruments should be traded, the rebalancing frequency, and the delta risk exposure.
- The marginal contribution of the volatility strategy to the risk of the investor’s portfolio and the contribution to the risk performance over the investor’s benchmark.
In this note, I will describe a quantitative approach along with back-test simulations to answer these questions to make the allocation decision. I will present a few examples and draw interesting conclusions.
Algorithmic strategies for investing in volatility
Asset universe
I will only consider the volatility carry strategies which involve selling and shorting the volatility to capture the volatility risk-premia. I will deal with products linked to the volatility of the S&P 500 index given its depth and liquidity and will consider the three algorithmic strategies.
- Put strategy which involves selling one month at-the-money put option on the S&P 500 index on the third Friday of each month. This strategy is similar to PutWrite algorithmic index designed by CBOE.
- Strangle strategy which involves selling one month out-of-the money put option with the option delta of about -20 and out-of-the money call option with the option delta of about 20. In essence, the strategy is close to the Condor algorithmic index provided by CBOE.
- VIX strategy which selling constant maturity one month VIX future. This strategy is similar to inverse VIX ETFs such as XIV ETF designed by Velocity Shares.
In table 1, I provide some details about these strategies.
Table 1. The description of the algorithmic strategies
| Asset | Implemen-tation | Source of Profit | Source of Loss | Pro | Cons |
| Put | Sell ATM puts | Put Premium | Realized negative performance of the S&P 500 index | Simple play on volatility premium | Significant delta exposure |
| Strangle | Sell 20-delta puts and calls | Put and call premiums | Realized negative and positive price performance beyond one standard deviation | i) Delta-neutral at the inception
ii) Exposure to skew and convexity risk-premiums |
Disproportionately sensitive to tail events |
| VIX | Sell 1st and 2nd month VIX futures | Contago premium | Positive performance of the VIX | Simple play on volatility term premium | i) Dependent on contago / backwardation
ii) Significant beta to the S&P 500 index in tail events |
The key attribute of these strategies is the source of the profit-and-loss.
- The Put strategy is a play on both the positive performance of the S&P 500 index as it has a significant delta exposure (about 50% at the inception on each month) and the volatility premium measured by the difference between the realized volatility and market implied volatility for at-the-money options. The expected and realized long-term performances of the S&P 500 index are positive because of the equity-risk premium, while the market implied volatility overestimates the realized volatility over long-term horizons. As a result, this simple strategy tends to outperform the S&P 500 index in the long-term. According to this study sponsored by the CBOE, since mid-1986 to 2012, the total realized return on the CBOE put strategy is 10.4% per annum vs 9.3% annualized total return on the S&P 500 index. Yet Put index has smaller volatility and drawdowns than the S&P 500 index.
- The Strangle strategy is a play on market implied volatilities for out-of-the money puts and calls. This strategy is about delta-neutral at the inception in each month and benefits from higher skew for index puts and implied convexity for puts and calls.
- The VIX strategy is a play on the contago in the term structure of VIX futures. The contago effect is produce by expectations of higher volatility in the future and higher hedging costs for the future uncertainty. Given that the volatility is mean-reverting over long periods of time, the only contributor to the VIX strategy is the roll yield associated with the contago effect, which is about 90% in annual terms.
Design of hedging strategies
Compared to other asset classes, volatility strategies tend to exhibit higher drawdowns relative to their historical volatilities and strongly negative skewness of realized returns. As a result, implementation of these strategies requires the design of the systematic hedging algorithms.
For each asset, I will consider the following hedging approaches:
- Vanilla: no hedging is performed, the strategy executes rolls systematically at each rebalancing day.
- Filter: the statistical relative value of the strategy is computed at each roll date. The relative value involves applying a time series model which uses data strictly prior to the roll date and computing the expected value of the roll based on the available historical information. If the expected value of the strategy is less than defined threshold, the roll is not executed at given rebalancing date. The filter enables to make a quantitative judgment about the expected profitability of each roll given prior historical information. If the expected performance falls below the desired threshold, the roll is not executed. No hedging is executed through the life of the roll.
3a. Filter+Hedge: the strategy applies the filter as described above. If the roll passes the filter, the strategy will sell options and implement the delta-hedging strategy upto the option expiry. The delta-hedging strategy is only applied for the PUT and Strangle strategies which involve trading in options directly and have well-defined delta exposure.
3b. Filter+ Long/Short: this strategy applies only for the VIX strategy. First the strategy applies the filter and, dependent on the signal strength, it enters either short (when the VIX futures term structure is in contago) or long positions (when the VIX futures are in backwardation).
In table 2, I present the summary of the nine strategies. For the ease of visualization, I will use red color for strategies with no hedge, blue color for the strategies with the statistical filter,and green color for strategies with the filter and hedge.
Table 2. Characteristics of the hedging strategies
| Strategy name | Underlying | Statistical Filter? | Delta-Hedged? | Long/Short? |
| Put | S&P 500 ATM Put | No | No | Short |
| Strangle | S&P 500 OTM Put and Call | No | No | Short |
| VIX | 1st and 2nd month Vix future | No | No | Short |
| Put+Filter | S&P 500 ATM Put | Yes | No | Short |
| Strangle+Filter | S&P 500 OTM Put and Call | Yes | No | Short |
| VIX+Filter | 1st and 2nd month Vix future | Yes | No | Short |
| Put+Filter
+Hedge |
S&P 500 ATM Put | Yes | Yes | Short |
| Strangle+Filter
+Hedge |
S&P 500 OTM Put and Call | Yes | Yes | Short |
| VIX+Filter
+Long/Short |
1st and 2nd month Vix future | Yes | No | Long/Short |
Volatility targeting
To align the risk-profile of each strategy and make meaningful comparisons, I will apply the volatility targeting with the annual volatility target set to 10%.
The volatility targeting is implemented in the two steps:
- The unleveraged strategy is implemented. For the put and strangle strategies, the number of option contract is computed at each roll date as the strategy funds divided by the put strike. The number of contract for the VIX futures is computed as the ratio of strategy fund to the price of the constant maturity one month VIX futures. As an illustration, the realized historic volatility is about 10% for Put strategy, 5% for Strangle strategy, and 50% for the VIX strategy.
- The master strategy is created by allocating to the unlevered strategies with the leverage determined to target the long-term volatility of 10% per annum. The volatility of each of the unleveraged strategies is computed at each roll dates using the time series strictly prior to the roll. The volatility of the strategy with the relative value filter is computed only when strategies have open positions.
Back-tested performance of individual strategies
I use the period from January 2005 to September 2017 (the VIX futures trading started in October 2005). As the benchmarks, I use the three assets:
- The S&P 500 index (labelled as S&P500) with the performance computed using ETF SPY.
- 20 year US treasury bonds (labelled as USbonds20y) with the performance computed using ETF TLT.
- The 50%/50% portfolio including the S&P 500 index and 20 year US treasury bonds (labelled as S&P500/USbonds20y) implemented using ETFs SPY and TLT, respectively, with monthly rebalancing to keep the constant 50%/50% exposure.
The realized total performance of the benchmarks includes dividends distributed by these ETFs.
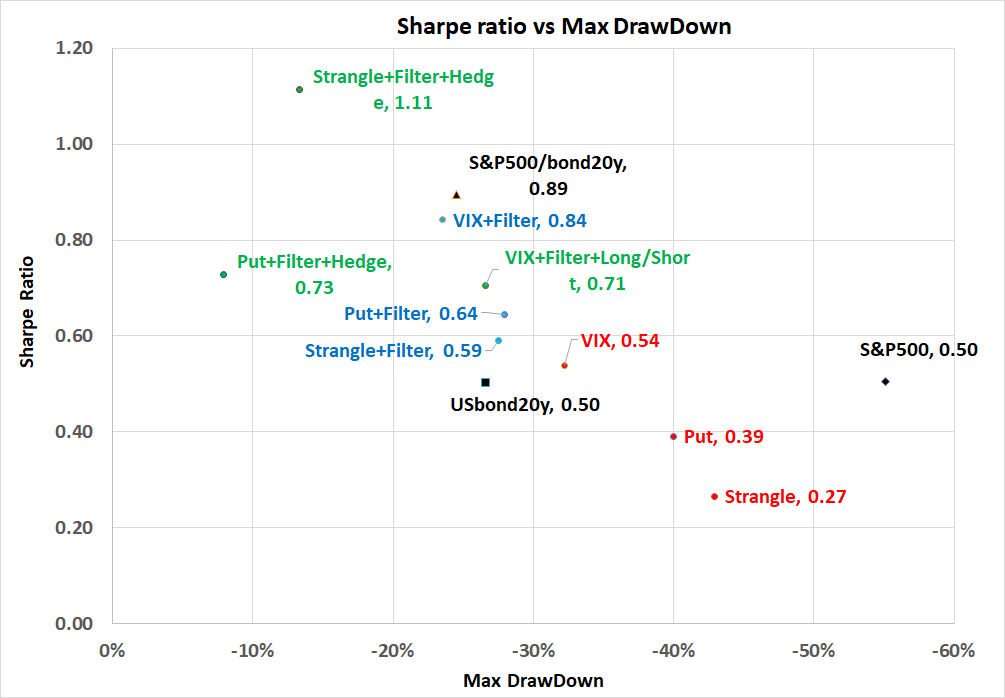
In table 3, I show the back-tested performance of the volatility strategies. Figure 1 illustrates the Sharpe ratio vs the maximum drawdown. Figure 2 illustrates the strategy alpha vs beta. The alpha and beta are estimated by regressing the monthly performance of the strategy explained by the monthly performance of the S&P 500 index. The monthly alpha from the regression is annualized. Table 4 reports the realized correlation matrix of monthly returns on these strategies.
Table 3. The back-tested performance of volatility strategies from 2005 to September 2017

Notations: Return is the total annualized return. Vol is the volatility of monthly returns. Sharpe is the Sharpe ratio using monthly volatility. Skewness and Kurtosis are the skewness and excess kurtosis of monthly returns, respectively. Max DD and Max DD recovery are the maximum drawdown and days to recover from it, respectively. Alpha and Beta are the coefficients of the regression of monthly returns on the strategy against the monthly returns on the S&P 500 index; the reported alpha is the annualized.
Figure 1. Backtested Sharpe ratio vs max drawdown

Figure 2. Strategy alpha vs beta computed by regressing monthly performance of the strategy explained by the monthly performance of the S&P 500 index.

Table 4. The correlation matrix of realized monthly returns.

Analysis
Vanilla strategies produce Sharp ratio comparable to the S&P 500 index but with smaller drawdowns. They have beta about 0.5 to the performance of the S&P 500 beta and insignificant alpha. They are also strongly correlated among each other with average correlation of 0.7.
The strategies with filter improve the Sharpe ratio twofold and reduce the drawdown by about 50%. They also produce a smaller beta of about 0.2 to the S&P 500 index with statistically significant alpha. Their average pair-wise correlation is about 0.5 indicating that opportunities and signals are relatively correlated.
The strategies with the filter and delta-hedging produce the strongest risk adjusted performance with very small beta and significant alpha. Their pairwise correlation is 0.25 indicating a potential diversification benefit by allocating to the basket of these strategies. The VIX strategy with Long/Short exposures has actually produced the negative correlation and betas to all three benchmarks, so that it can serve as a good diversifier for equity portfolios.
Return Decomposition into the Factor Model
I apply the four factor Fama-French-Carhart model to relate monthly returns on the strategies into the monthly returns on the market factor (MRK), the size factor (SML), the book-to-market value factor (HML), and momentum factor (UMD). I use the AQR data for monthly returns on the factors estimated using US stocks.
Table 5 reports the estimated coefficients of the 4-factor model. We see that all strategies have insignificant exposures to the style factors. Only the put strategy has a significant exposure to the momentum factor, which is intuitive. The exposure to the market factor is significant for vanilla strategies, while it reduces considerably for the strategies with the filter. The strategies with the delta-hedge have insignificant exposure to the market factor.
Table 5. Estimated exposures to Fama-French-Carhart 4-factor model using monthly returns from 2005 to September 2017

Notations: Alpha is the annualized alpha, MRK is the beta to the market factor, SMB is the beta to the capitalization factor (small minus big), HML is the beta to the book-to price value factor (high minus low), is the beta to the momentum factor (up minus down). R^2 is the explanatory power of the regression. The value of the t-statistics is provided in the parentheses. Significant estimates are marked with *.
Back-tested performance on the portfolio level
Now I consider the impact of the volatility strategies on the portfolio level. Again, I use the three benchmarks. For each of the tree benchmarks, I assume that 10% of the total funds are allocating to any of the 9 strategies separately with monthly rebalancing.
I define the alpha as the regression of the monthly performance of the 90%/10% portfolio invested in the benchmark and the volatility strategy, respectively, explained by the monthly performance of the respective benchmark. The annualized alpha of this regression indicates the marginal contribution of the volatility strategy to generation of the alpha for the benchmarked portfolio.
Figure 3 shows the contribution to the portfolio alpha. Figure 4 shows the % increase in the Sharpe ratio of the 90%/10% portfolio invested 90% in the benchmark and 10% in the strategy against vs 100% portfolio wholly invested in the benchmark.
Figure 3. Contribution to the portfolio alpha for thee benchmarks

Figure 4. % Increase in the Sharpe ratio of the 90%/10% portfolio invested 90% in the benchmark and 10% in the strategy against vs 100% portfolio wholly invested in the benchmark.

Analysis
Vanilla strategies have a small risk-adjusted contribution to portfolio benchmarked to the S&P 500 index or 50/50 portfolios. However, they do produce significant contribution to portfolios benchmarked to UST bonds. This is because they have equity overlay with helps to off-set the rates risk in bullish market conditions.
The strategies with the filter produce significant contribution to portfolios benchmarked to the S&P 500 index. Furthermore, they improve the risk-adjusted contribution to fixed-income portfolios by reducing the downside of the equity overlay.
The strategies with the filter and delta-hedge have a mixed contribution: the put strategy has a stronger correlation to the S&P 500 in tail events so its marginal contribution is relatively modest. Both Strangle and VIX strategies has a significant improvement of the risk-profile for all of the three benchmarks.
Conclusions
Well-designed algorithmic strategies provide transparent solutions for investing to volatility risk-premia. The risk profile and delta exposures must be explained to investors and tailored to their portfolios and benchmarks. The volatility strategies with statistical filtering can be applied as overlays in fixed-income portfolios. The delta-hedged option strategies and long-short VIX futures strategies can be applied as absolute return strategies in allocations to alternatives.
4 thoughts on “Allocation to systematic volatility strategies using VIX futures, S&P 500 index puts, and delta-hedged long-short strategies”
Pingback: Selling volatility in a low volatility regime: the current level of the volatility is not a predictor for future performance | Artur Sepp Research Blog
Pingback: Lessons from the crash of short volatility ETFs | Artur Sepp Research Blog: Volatility Modelling and Trading
Pingback: Trend-following strategies for tail-risk hedging and alpha generation | Artur Sepp Research Blog: Quantitative Investment Strategies
Panagiotis
Very interesting post Artur.
I have a couple of questions below:
1) It would be interested to rerun those backtests and display the performance of the strategies in 2018. I’m particularly curious to see how the VIX strategy would have performed during Feb 2018.
2) I am not sure I understand how the statistical filter is applied in practice. More specifically, could you give some examples regarding the time series models that you used for the backtest?Moreover,it’s not clear to me how the expected value of the strategy is calculated in order to make the decision of rolling or not.
I would highly appreciate it if you could elaborate a bit on the above.
Thank you for your insightful posts.
Panagiotis